バラエティテレビ番組で、ある人が、その人と全く面識がない有名人と、知人をたどっていきながら、つまり数珠つなぎ的にたどっていけば、何人でつながるのか、つながらないのかという実験を行っていました。なかなか実際に合うことが出来ない、つまりつながりを実感できないコロナ禍にあって、妙に記憶に残る番組でした。確か、間に4人、あるいは5人を入れれば、その有名人につながって番組内の会場を沸かしていました。

フォロワーが数万人であるSNSを有する人も珍しくなくなった現在のネット社会、ネットで知り合いをたどっていけば一人ぐらいはすぐに有名人にたどり着けそうですが、それでも特定の有名人、たとえばジョー・バイデン米大統領や俳優のブラッド・ピットに容易につながるかというと疑問を呈するでしょう。しかし、これがつながるのです。先のバラエティ番組のように間に高々6人を介することで、誰にでも繋がってしまうのです。もちろん、必ずとは言えませんが、高い確率でつながってしまうのです。これは「六次の隔たり」と呼ばれています。数学的に証明されているわけではありませんが、肯定的に信じられている仮説です。スモールワールド現象とも呼ばれ、日本語に訳するとすれば、「世間は狭い」という現象です。

たとえば、ツイッターのフォロワーで考えると、特定の有名人が自分のフォロワーになっている可能性は極めて低い、一般の人にはほとんど有りえないと言って良いでしょうが、そのフォロワーのフォロワーと言うように孫のフォロワーまで考えると少しは可能性が高くなります。フォロワーのフォロワーのフォロワーのフォロワー、つまり玄孫（やしゃご）フォロワーまで考えると確率60％以上でつながっていることが言えるのです。

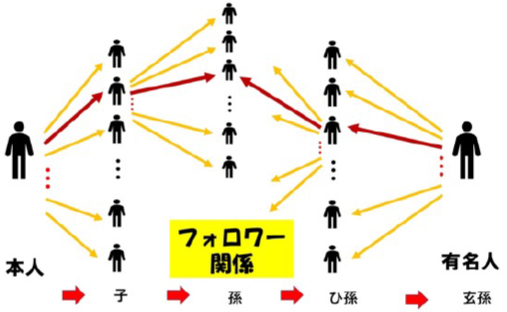
一見無関係な2人のユーザのそれぞれのフォロワー数をa,bとします。ツイッターの総ユーザ数をｎとしたとき、それぞれのフォロワーで重複がある、つまり同一のフォロワーである確率Ｐの概算値は以下で与えられます。

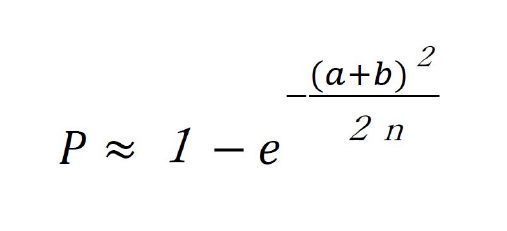
ツイッターの実行ユーザ数（月間ユーザ数）は3億人と言われています。一人当たり平均して、400人程度のフォロワーがいると報告されています。この値を上の式に代入するとほぼ０に近い値になります。しかし、フォロワーのフォロワー、つまり起点（自分）から見て、孫に当たるフォロワーを考えると約16万人となります。半分ほどが重複していると考えて、それを除く、約8万人の孫に当たる新たなフォロワーが存在したとすると、その孫同士で同一のフォロワーである確率は60％を超えることになります。つまり一見無関係なユーザがそれぞれの孫にあたるフォロワーを介してつながっていることになるのです。しかし、実際には親と子のフォロワーの関係はその属性が互いに大きく依存していることが多く、フォロワーの半分は全く独立と仮定しても、玄孫では難しく、その子、その孫、つまり来孫（らいそん）、昆孫（こんそん）ぐらいになるかもしれません。六次の隔たりです。

これは「誕生日の問題」と密接に関係しています。誕生日の問題とは、何人集まれば、生まれた年は別にして、月日が同じ誕生日の人がいるかという問題です。単純に考えれば、1年は365日ですから、300人ぐらい集まれば、同じ誕生日の人がいるだろうと予想されます。しかし実際は23人集まれば、確率50％で同じ誕生日の人が存在するのです。40人も集まれば、ほぼ確実に同じ誕生日の人が存在するのです。数十人が集まったコンパで、たまたま同じ誕生日の人がいても、それは「奇跡の出会い」ではなく、よくあることなのです。

また「誕生日攻撃(birthday attack)」と呼ばれる暗号解読とも関係しています。上式はｎ個の値の集合から、一様かつ無作為に、重複を許し(a+b)個選んだとき、少なくとも1つの値が2回以上選ばれる確率の概算式です。つまり鍵を推定する際に、暗号文から平文に戻る鍵を直接求めるのではなく、暗号文から平文に戻る過程の中間鍵の候補と、逆に平文から暗号にさかのぼる中間鍵の候補を観測し、一致する鍵を求めるのです。